三角測量(Triangulation)
- 三角測量の概要
- 三角網を配置し,一つの辺については精密に距離を計測しておく(太線).これを基線という.他の点の座標については,角度の計測によって求めていく.三角形の内角の和が180°であることで,誤差を調整することができる.広範囲を測量する時に用いられ,三角点は見晴らしの良い場所に設置される.
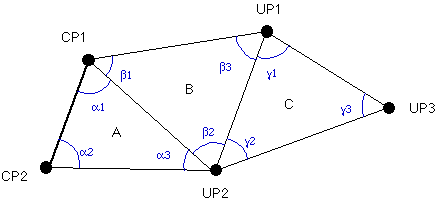
- 上図において,CP1とCP2は,座標が既知の基準点である.これらの基準点をもとに未知の点のUP1〜UP3の座標を構成される三角形のすべての内角を測量することによって求めるのである.
- 測量方法
- 三角形の頂点にセオドライトをセッティングし,すべての角度を測っていく.
- 角度は正と反にて測量し(後述),その平均をとる.
- CP2とUP3では,一つの角度を測量するだけでよいが,それ以外の点では複数の角度を測量する必要がある.このとき,測量可能なすべての角度を正反で測量しなければならない.
- UP2を例に測量する必要のある角度を以下に示す.
- 角CP2 - UP2-
CP1....(α3)
- 角CP1 - UP2-
UP1....(β2)
- 角UP1 - UP2-
UP3....(γ2)
- 角CP2 - UP2-
UP1....(α3+β2)
- 角CP1 - UP2-
UP3....(β2+γ3)
- 角CP2 - UP2-
UP3....(α3+β2+γ3)
- 測点まわりの誤差の調整
- 複数の角度を測量した測点については,最小二乗法によって角度の最確値を求める.UP2を例に手順を示す.
- α3,β2,γ3の最確値をA3,B2,C3とすると,誤差は以下となる.
- A3−α3
- B2−β2
- C3−γ3
- A3+B2−(α3+β2)
- B2+C3−(β2+γ3)
- A3+B2+C3−(α3+β2+γ3)
- したがって誤差の二乗和Φは以下となる.
- Φ=(A3−α3)2+(B2−β2)2+(C3−γ3)2+{A3+B2−(α3+β2)}2+{B2+C3−(β2+γ3)}2+{A3+B2+C3−(α3+β2+γ3)}2
- Φが最小となるA3,B2,C3を計算するには,A3,B2,C3で偏微分して連立方程式を計算すればよい.
- ∂Φ/∂A3 = 0
- ∂Φ/∂B2 = 0
- ∂Φ/∂C3 = 0
- 各三角形での誤差の調整
- 三角形の内角の和は180°であるが,測量結果には誤差が含まれている.その誤差を考慮し,和が必ず180°となるように調整する.
- 三角形Aを例に解説する.誤差Φは以下のように計算できる.
- Φ =180− α1−α2−α3
- このΦを3つの角に分配するため角度の数3で除算し,それを各角度に加える.
- 三角形の辺長の計算
- 座標変換
- ここまでで,やっと構成する三角形の全ての内角と辺の長さが求まった.さらに続けてしなければならないのは,三角形を構成するすべての頂点の座標を計算することである.
- 基準点CP1とCP2の座標は与えられているので,この基準点座標をもとに座標変換をすれば,計算できる.その手法を以下の図を用いて解説する.この図では,基準点をA,Bとし,未知点Qの座標を求めること対象としている.
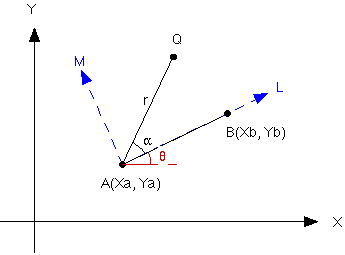
- 基準点AよりQを視準し,角度がα,距離がrという結果を得た.このとき,線分ABを軸とするLM座標系におけるQの座標(Lq,
Mq)は,角度αを時計まわりの方向を正とするとき,以下の式で表すことができる.この図では,αは負の値を取る.
- Lq = r cosα
- Mq = - r sinα
- このLM座標系で表された座標をXY座標系に変換するには,X軸とL軸とのなす角度θだけ回転させ,基準点Aの座標分平行移動させればよい.したがって求める座標(Xq,
Yq)は,次式で表すことができる.
- Lq cosθ - Mq sinθ + Xa
- Lq sinθ + Mq cosθ + Ya
- ここで,θ= atan((Ya - Yb)/(Xa -
Xb))

